NUMEROS INDICES ¿PARA QUE SIRVEN?

NUMEROS INDICES

¿PARA QUE SIRVEN LOS NUMEROS INDICES?

Los números índices nacen de la necesidad de conocer en profundidad la magnitud de un fenómeno y poder realizar comparaciones del mismo en distintos territorios o a lo largo del tiempo. Una forma inicial de resolver el problema es referir cada situación a la anterior, pero esto no hace viable la posibilidad de comparaciones significativas, al menos directamente, salvo en lo concerniente a dos de ellas inmediatas. Por esto es más conveniente escoger una situación determinada como punto de referencia inicial, para remitir a ella todas las demás observaciones, esta situación se denomina situación base y las comparaciones que se realizan vienen establecidas a través de un número índice. Los números índices, o simplemente índices, proporcionan comparaciones entre datos correspondientes a diferentes situaciones, escalonadas con arreglo a algún criterio conocido (por ejemplo, por el transcurso del tiempo).
Si definimos a 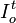como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces

donde representa el valor del bien en el período t y el valor del bien en el periodo o.
Las comparaciones, en estadística, entre distintas variables o entre los valores de una sola variable pueden realizarse de distintas formas. Las formas más simples son las que se llevan a cabo por diferencia o aquellas que se realizan por cociente. Estas últimas tienen la ventaja frente a las primeras que eliminan el problema de las unidades de medida. En cambio el segundo de los procedimientos, aunque no adolece de ese problema, puede plantear problemas relativos a elegir la unidad de referencia para realizar las comparaciones.

 Propiedades

Uno de los problemas de mayor importancia a la hora de elaborar un número índice es el conseguir que éste sea adecuadamente representativo, para ello es preciso que el índice cumpla ciertas propiedades de carácter matemático y reúna ciertos requisitos en su definición:

1. Identidad. Cuando el período base y el de comparación coinciden, el índice debe ser igual a uno.
2. Inversión. Si en un índice se invierten los períodos base y de comparación, el índice toma el valor recíproco al anterior.
3. Circular. Si se multiplica el índice de un período Z con relación a un período Y por el índice de Y con relación a X, el producto ha de ser el índice de Z con relación a X.
4. Existencia. El índice ha de tomar valores reales y finitos para cualquier valor de la variable observada.
5. Proporcionalidad. El índice elaborado sobre unos determinados valores de una variable ha de ser proporcional al índice correspondiente a los valores de esa variable multiplicados por un mismo número K.
6. Variación proporcional. Si los valores de la variable varían en una cierta cuantía, el índice varía proporcionalmente.
7. Inalterabilidad. Si se introduce una nueva modalidad en el índice complejo, de tal manera que el valor de éste coincide con el del índice simple de aquella, el índice complejo no varía.
8. Homogeneidad. El valor de un índice no ha de ser afectado por modificaciones de las unidades de medida.