jueves, 22 de noviembre de 2012

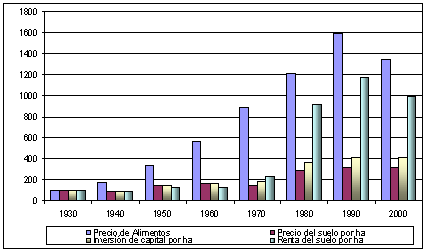
TIPOS DE NúMEROS INDICES

Índices simples y complejos

Cuando se realiza una comparación entre los valores de una sola magnitud se obtienen índices simples, En cambio, si se trabaja con más de una magnitud a la vez, se habla de índices complejos. En los dos casos se comparan siempre dos situaciones, una de las cuales se considera como referencia. Cuando se trata de comparaciones temporales, a la situación inicial, se le conoce como periodo base o referencia, mientras que el periodo objeto de comparación se denomina corriente o actual. Para elaborar un número índice de carácter simple, se asigna al periodo que es objeto de referencia el valor 100, de esta manera los números índices de las distintas observaciones posteriores, no son otra cosa que porcentajes de cada valor con respecto al de la referencia. Dentro de los índices complejos se distingue entre índices ponderados y no ponderados, según el peso que se le de a los distintos valores

CALCúLO DE NúMEROS INDICES

El cálculo considera 2 métodos para elaborar índices : El No ponderado y El Ponderado

(1) INDICES NO PONDERADOS O INDICES SIMPLES

1.1.- Indice Simple de Precios o Precio relativo (Ip)

Mide la variación en el precio de un solo artículo en el período dado (t) con respecto al período base (o)

Ip = Pt x 100

Po

1.2.- Indice Simple de Cantidades o Cantidad relativa (Iq)

Iq = qt x 100 qo = Cantidad del bien en el período dado

qo qt = Cantidad del bien en el período base

Ejemplo 2:

(2) INDICES COMPUESTOS (Agregados, Ponderados)

2.1.- Indices agregados simples de precios y cantidades.

P = Pti Q = Qti

Poi Qoi

Desventaja del índice : No considera ponderaciones ni medidas en distintas

Unidades

Indices alternativos : Pp = (Pti/ Poi) Qp = (Qti/Qoi)

NUMEROS INDICES ¿PARA QUE SIRVEN?

NUMEROS INDICES

¿PARA QUE SIRVEN LOS NUMEROS INDICES?

Los números índices nacen de la necesidad de conocer en profundidad la magnitud de un fenómeno y poder realizar comparaciones del mismo en distintos territorios o a lo largo del tiempo. Una forma inicial de resolver el problema es referir cada situación a la anterior, pero esto no hace viable la posibilidad de comparaciones significativas, al menos directamente, salvo en lo concerniente a dos de ellas inmediatas. Por esto es más conveniente escoger una situación determinada como punto de referencia inicial, para remitir a ella todas las demás observaciones, esta situación se denomina situación base y las comparaciones que se realizan vienen establecidas a través de un número índice. Los números índices, o simplemente índices, proporcionan comparaciones entre datos correspondientes a diferentes situaciones, escalonadas con arreglo a algún criterio conocido (por ejemplo, por el transcurso del tiempo).
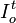Si definimos a $I^t_o$ como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces
$I^t_o = \frac{x_t}{x_o}$
donde $x_t$ representa el valor del bien en el período t y $x_o$ el valor del bien en el periodo o.
Las comparaciones, en estadística, entre distintas variables o entre los valores de una sola variable pueden realizarse de distintas formas. Las formas más simples son las que se llevan a cabo por diferencia o aquellas que se realizan por cociente. Estas últimas tienen la ventaja frente a las primeras que eliminan el problema de las unidades de medida. En cambio el segundo de los procedimientos, aunque no adolece de ese problema, puede plantear problemas relativos a elegir la unidad de referencia para realizar las comparaciones.

Propiedades

Uno de los problemas de mayor importancia a la hora de elaborar un número índice es el conseguir que éste sea adecuadamente representativo, para ello es preciso que el índice cumpla ciertas propiedades de carácter matemático y reúna ciertos requisitos en su definición:

Identidad. Cuando el período base y el de comparación coinciden, el índice debe ser igual a uno.
Inversión. Si en un índice se invierten los períodos base y de comparación, el índice toma el valor recíproco al anterior.
Circular. Si se multiplica el índice de un período Z con relación a un período Y por el índice de Y con relación a X, el producto ha de ser el índice de Z con relación a X.
Existencia. El índice ha de tomar valores reales y finitos para cualquier valor de la variable observada.
Proporcionalidad. El índice elaborado sobre unos determinados valores de una variable ha de ser proporcional al índice correspondiente a los valores de esa variable multiplicados por un mismo número K.
Variación proporcional. Si los valores de la variable varían en una cierta cuantía, el índice varía proporcionalmente.
Inalterabilidad. Si se introduce una nueva modalidad en el índice complejo, de tal manera que el valor de éste coincide con el del índice simple de aquella, el índice complejo no varía.
Homogeneidad. El valor de un índice no ha de ser afectado por modificaciones de las unidades de medida.

NUMEROS INDICES

Número índice

¿QUE SON?

Un número índice es una medida estadística que permite estudiar las fluctuaciones o variaciones de una magnitud o de más de una en relación al tiempo o al espacio. Los índices más habituales son los que realizan las comparaciones en el tiempo, por lo que, como veremos más adelante, los números índices son en realidad series temporales.

martes, 20 de noviembre de 2012

Índice de Gini

¿QUE ES?

El índice de Gini mide hasta qué punto la distribución del ingreso (o, en algunos casos, el gasto de consumo) entre individuos u hogares dentro de una economía se aleja de una distribución perfectamente equitativa. Una curva de Lorenz muestra los porcentajes acumulados de ingreso recibido total contra la cantidad acumulada de receptores, empezando a partir de la persona o el hogar más pobre. El índice de Gini mide la superficie entre la curva de Lorenz y una línea hipotética de equidad absoluta, expresada como porcentaje de la superficie máxima debajo de la línea. Así, un índice de Gini de 0 representa una equidad perfecta, mientras que un índice de 100 representa una inequidad perfecta.

¿PARA QUE SIRVE?

Normalmente se utiliza para medir la desigualdad en los ingresos, dentro de un país, pero puede utilizarse para medir cualquier forma de distribución desigual.

El coeficiente de Gini es un número entre 0 y 1, en donde 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos) y donde el valor 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno).

El índice de Gini es el coeficiente de Gini expresado en porcentaje, y es igual al coeficiente de Gini multiplicado por 100.

Aunque el coeficiente de Gini se utiliza sobre todo para medir la desigualdad en los ingresos, también puede utilizarse para medir la desigualdad en la riqueza. Este uso requiere que nadie disponga de una riqueza neta negativa.

COMO SE CALCULA?

El coeficiente de Gini se calcula como una proporción de las áreas en el diagrama de la curva de Lorenz. Si el área entre la línea de perfecta igualdad y la curva de Lorenz es a, y el área por debajo de la curva de Lorenz es b, entonces el coeficiente de Gini es a/(a+b).

Esta proporción se expresa como porcentaje o como equivalente numérico de ese porcentaje, que es siempre un número entre 0 y 1. El coeficiente de Gini se calcula a menudo con la Fórmula de Brown, que es más práctica:

Donde:

G: Coeficiente de Gini
X: Proporción acumulada de la variable población
Y: Proporción acumulada de la variable ingresos

De forma resumida, la Curva de Lorenz es una gráfica de concentración acumulada de la distribución de la riqueza superpuesta a la curva de la distribución de frecuencias de los individuos que la poseen, y su expresión en porcentajes es el índice de Gini